Fractal geometry is the underlying cosmological principle. But what exactly do I mean by fractal geometry? What is a self-similar pattern? And what do I mean when I talk about fractal dimensions? To understand this let us look at a simple example, the Koch snowflake, whose construction is predicated on a simple recursive algorithm.

A Koch curve has an infinitely repeating self-similarity when it is magnified.
The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows: First divide the line segment into three separate segments of equal length. Next draw an equilateral triangle where the middle line segment is the new triangle’s base with its tip pointing outwards. Then lastly remove the line segment that is the base of the new triangle. Thus, after one iteration of this process, the resulting shape is the outline of a hexagram. Repeating this process iteratively renders the Koch snowflake.
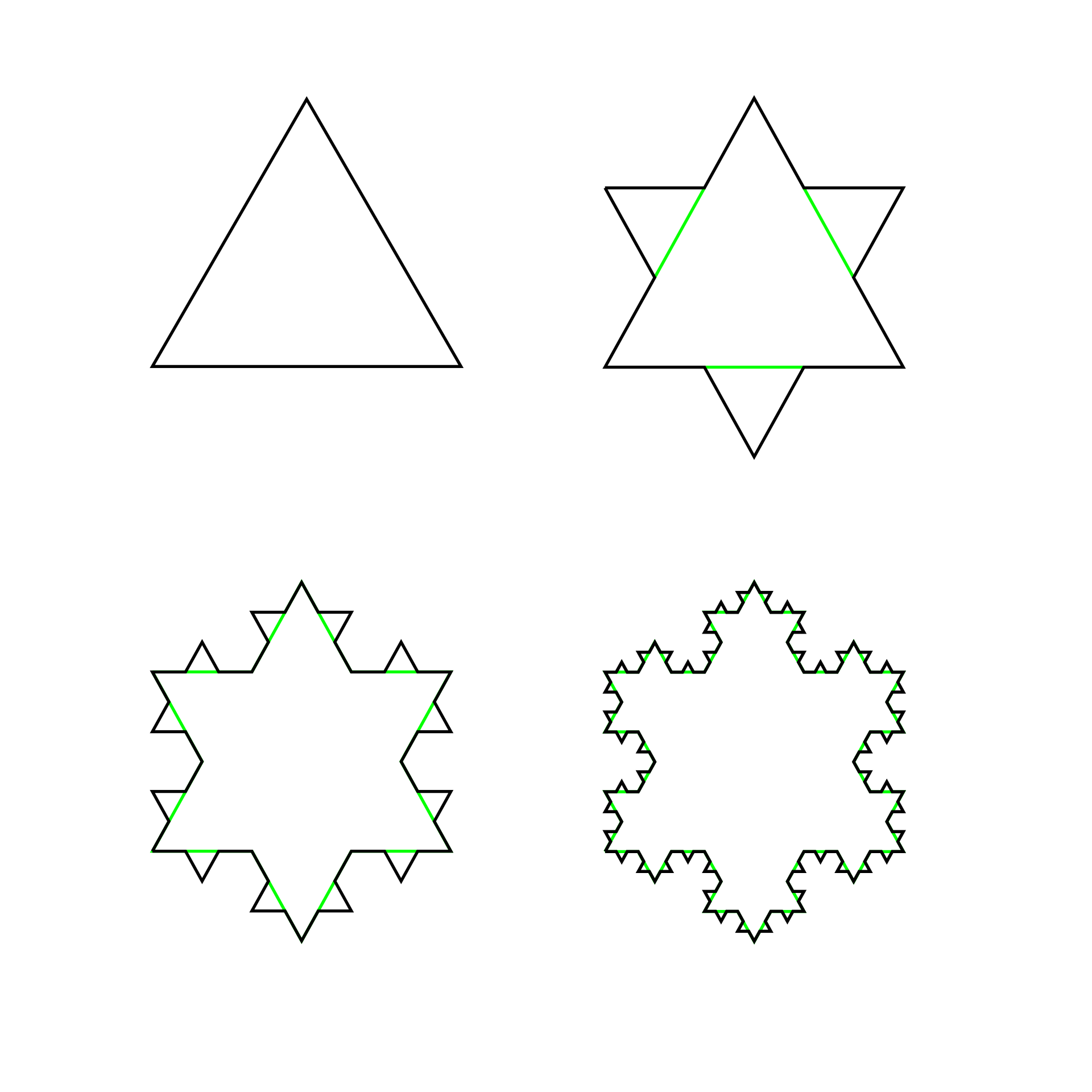
The first four iterations of the Koch snowflake.
So for the next iteration of this procedure: Again divide the line into three separate segments of equal length. Then draw an equilateral triangle, with the middle line segment acting as the base of the new triangle, with its tip pointing outwards. Lastly remove the middle line segment to complete the second iteration of the Koch snowflake algorithm. And as we proceed through all the other iterations the fractal curve that is the Koch snowflake comes into view.
A self-similar object is exactly or approximately similar to a part of itself. The self-similar pattern of the Koch snowflake is seen by taking one of the lines and dividing it into four parts. Each part is an exact copy of each other as well as a scaled down copy of the original whole. The length of each of the four parts is one third the length of the original whole.
The concept of a fractal dimension is defined by the duality in this division of the whole between both the length and scale. This dual concept in the division between length and scale is most easily seen in considering a line, a square and a cube.
A line can be divided equally into two new lines, each line, a copy of its original, scaled down by a factor of a half. A square can also be equally divided into four new squares. Each of these four new squares is an exact copy of the original square again scaled down by a factor of a half.
A cube can be divided into eight separate cubes each an exactly copy of the original but again its size is scaled by a factor of a half. This division into exact copies of the original whereby each copy is scaled by one half is done by length.
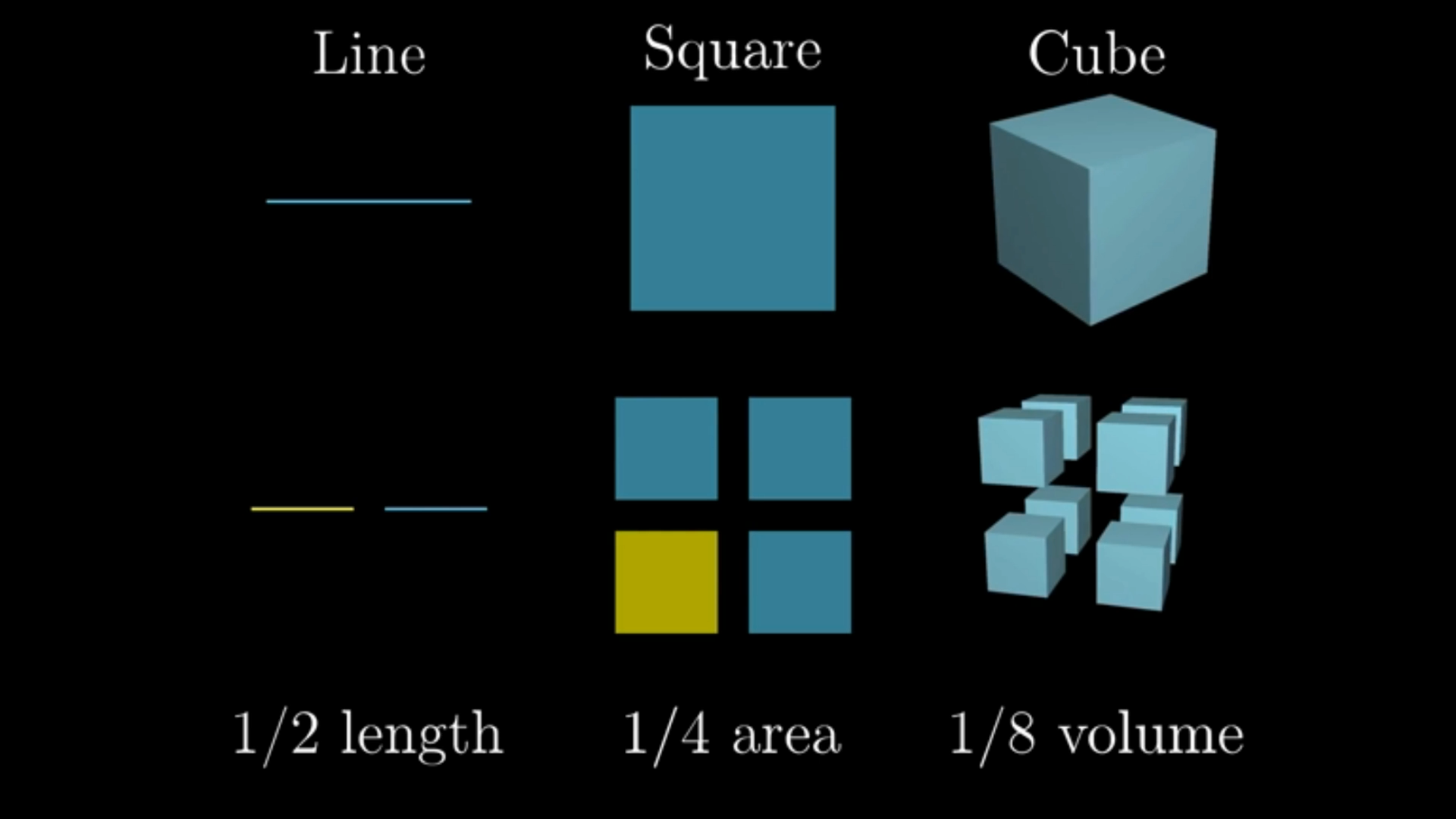
The division of a one dimensional line into two equal halves. Each line half is the same as the original whole but scaled by a half. The division of a two dimensional square both vertically and horizontally produces four new squares. Each is the same shape as the whole but scaled by a quarter. Finally, the division of a three dimensional cube both vertically, horizontally and depth-wise produces eight new cubes. Each cube is the same shape as the whole but scaled by an eighth.
Another way of looking at this scaling process in order to produce exact copies of itself is by mass. Imagine our line is a piece of wire that is cut equally to produce two new pieces of wire, each of equal length to one another. The mass, or weight, of each of the two new wires is one half of the original whole.
However for a square sheet of metal divided into four squares the weight and surface area of each square is one quarter of the original. And for a cube of metal divided equally into eight cubes the mass and volume of each is one eighth that of the original cube.
So we can say that when we scale down the length of the line by a half the mass of the line is in turn scaled by a half. Or one half to the power of one, as in one dimension, is equal to one half. Conversely when we scale down the length of a square the mass of the square is scaled by one quarter. Or one half to the power of two, as in two dimensional, is equal to one quarter. And when we scale down the length of a cube by one half the mass of the cube in turn is scaled by one eighth. Or one half, the length scaled, to the power of three, as in three dimensional, which is equal to one eighth, the mass scaled.

Dividing a length of the original whole by four we derive the exact same shape as the whole but scaled by a factor of one third. This is the essence of self-similarity in identifying the same pattern but at different scales. We get the fractal dimension by the power relationship between the mass scale and the length scale. Here it is \( 3^D = 4 \) which, after applying logarithms, means \( D \approx 1.262 \) .
It is in the “to the power of” relationship equating the scaling factor of length to the scaling factor of mass that the concept of what is meant by a fractal dimension is given definition. So for a two dimensional square when its length is scaled by some factor then the resultant mass, or weight, is equal to the length scaling factor raised to the power of two. And for a three dimensional cube when its length is scaled by some factor then the resultant mass, or weight, is equal to the length scaling factor raised to the power of three. It puts the three in three dimensional.
Returning to the Koch snowflake. Here the pattern of the whole is equally divided into four parts each of which is an exact copy of the whole. The length of each of the four parts is one third of the original whole. Hence we can say it is scaled in length by one third but scaled in mass by one quarter. Its fractal dimension “D” is “one third raised to the power of D such that it equals one quarter”. Applying logarithms we see that “D” is equal to around 1.262. Hence the fractal dimension of the Koch snowflake is equal to 1.262.
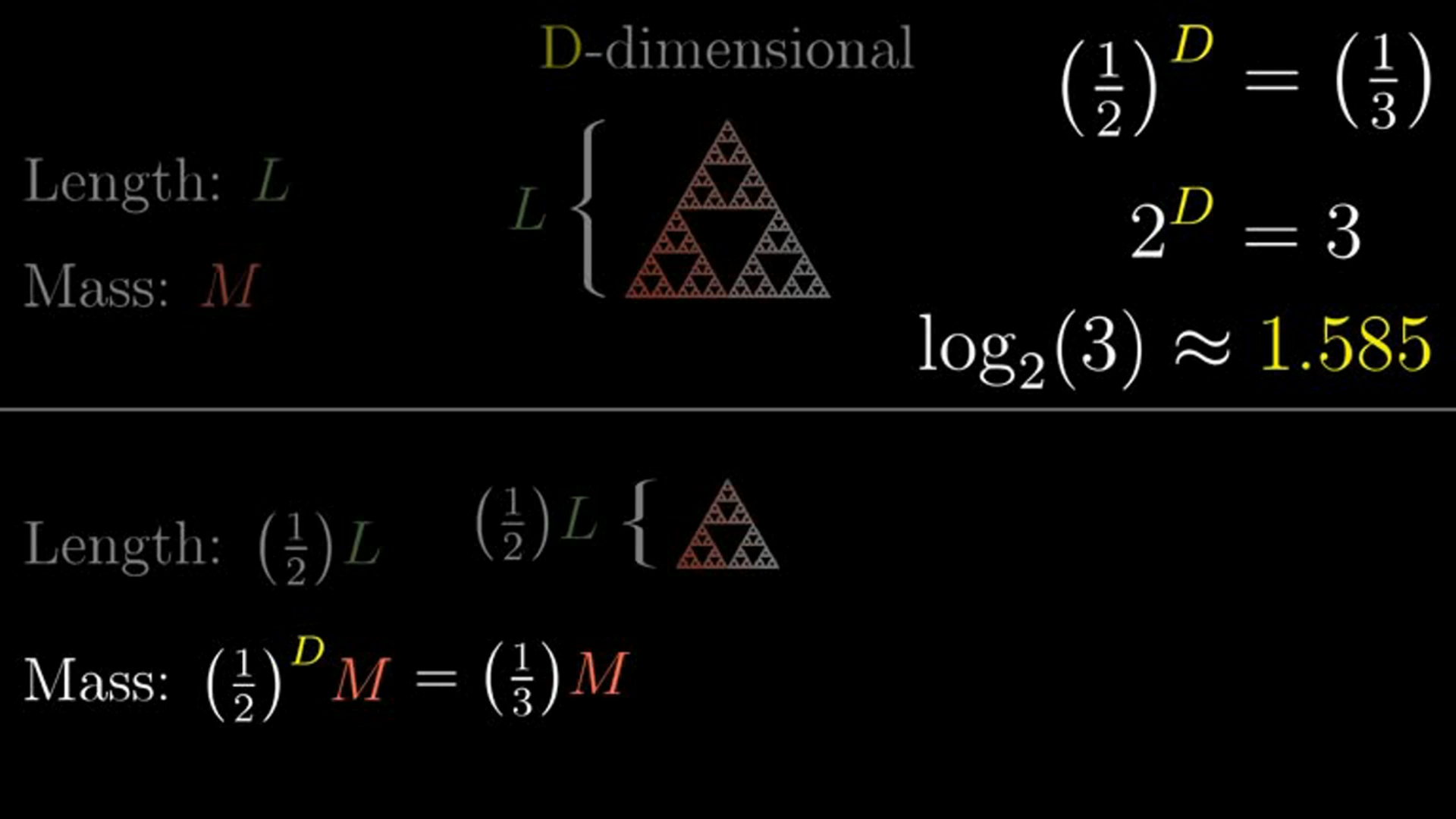
Dividing a length of the original whole by three we derive the exact same shape as the whole but scaled by a factor of one half. We get the fractal dimension by the power relationship between the mass scale and the length scale. Here it is \( 2^D = 3 \) which, after applying logarithms, means \( D \approx 1.585 \) .
Let’s look at another simple fractal curve; the Sierpinski triangle. Here when the Sierpinski triangle is scaled in length by a half it renders three copies of the original whole. Here the length is scaled by a half and the mass of each of the three parts is one third that of the whole. So its fractal dimension “D” is “one half to the power of D such that it equals one third”. Using logarithms we see that “D” is equal to around 1.585. Thus we say the fractal dimension of the Sierpinski triangle is 1.585.
As a rough analogy the measure of fractal dimension can be viewed as measurement of how rough a given curve is. This analogy is best seen when applied to the real world problem of measuring the length of a given coastline.
Take a coarse grid with the coastline of Britain drawn upon it and count the number of squares touched by the British coastline. Next zooming in on to the coastline of both England and Wales, repeating the same process, counting the number of squares touched by the coastline. Zoom in again and repeat the same box counting process.
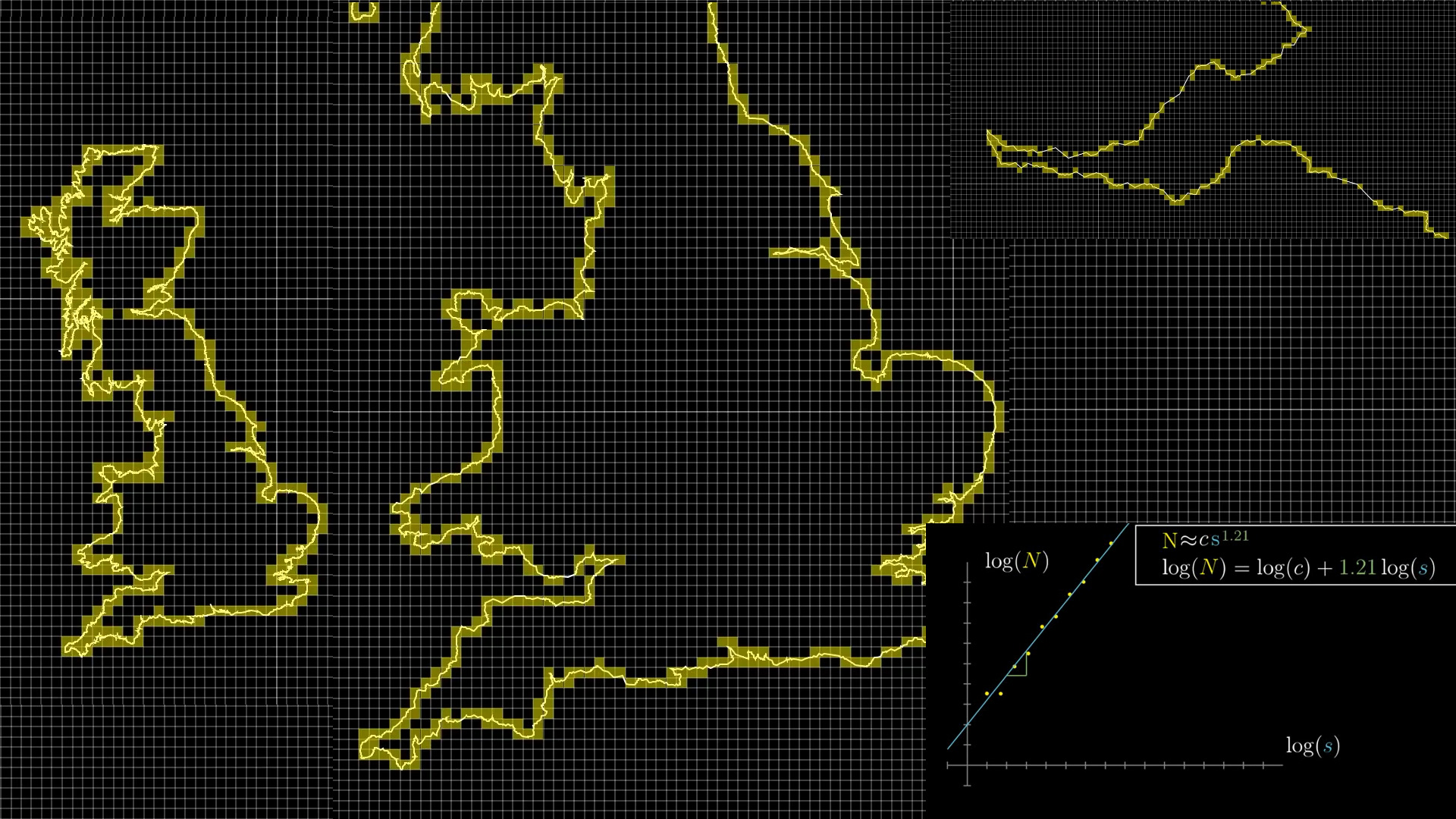
By counting the number of boxes touched by the British coastline at different scales we plot the logarithm of the count against the logarithm of the scale. We find a linear relationship in the graph whose gradient is the fractal dimension of the British coastline which is 1.21.
What we find is that the number of boxes touched by the coastline is roughly equal to a constant multiplied the scaling factor to the power of 1.21 which is the fractal dimension of the British coastline.
A curve is said to be a fractal if this relationship holds for any scale. In the case of the British coastline this has been shown to be the case where the fractal dimension is equal to 1.21. A rougher coastline, like Norway has a fractal dimension equal to 1.52.
Another example from nature is the surface of the sea. A relatively calm sea has a fractal dimension roughly equal to 2.05. This is in contrast to a stormy sea surface whose fractal dimension is roughly equal to 2.3. The larger the number the rougher the fractal surface or curve actually is.
If our universe is indeed fractal then what is its fractal dimension? Maybe its value is to be found when considering Lambda, the cosmological constant? Possible, but the first step is here is to try and identify the shape of the self-similar pattern from which the universe and beyond is formed.